LCM vs GCD: Key Differences with Practical Examples
Two sides of the same coin: understanding how they differ and how they connect.
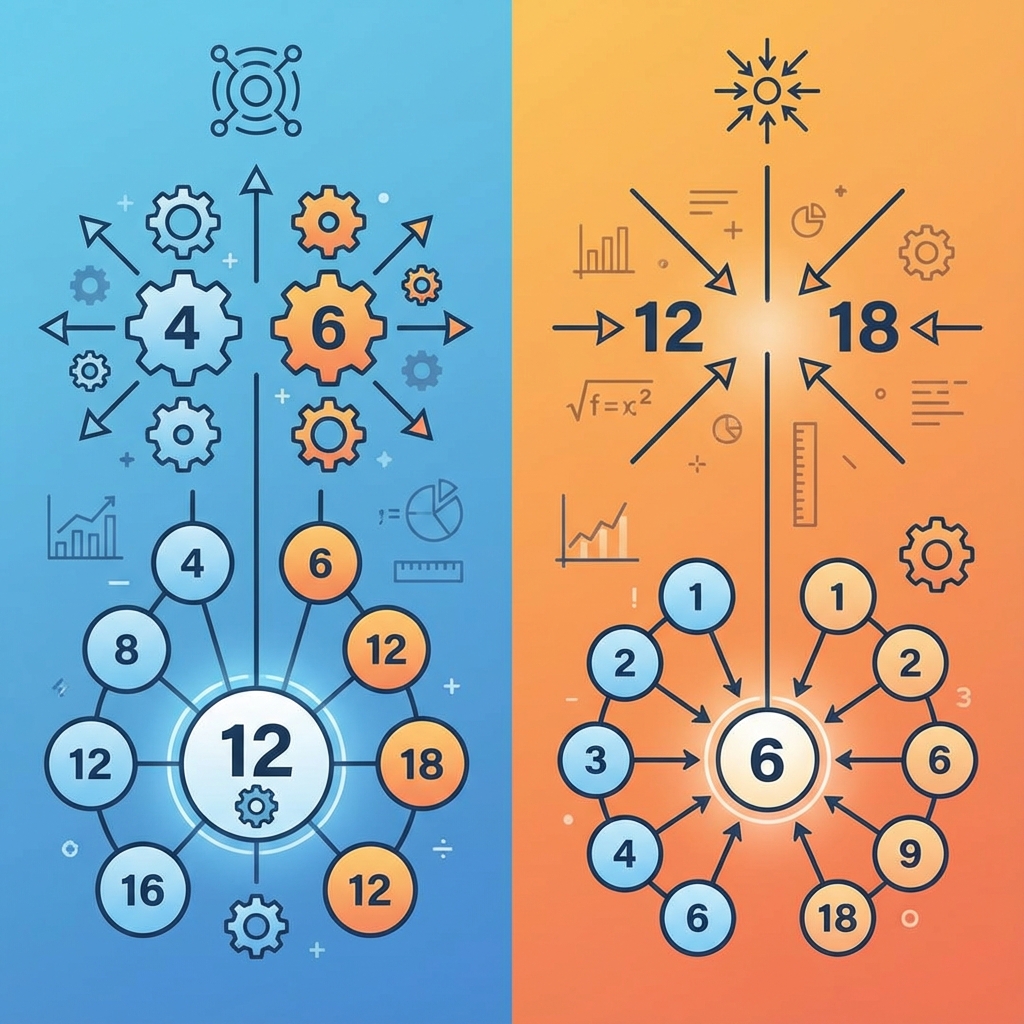
The Core Difference
While both concepts deal with relationships between integers, they look in opposite directions:
LCM (Least Common Multiple)
Looks UP at multiples. It finds the smallest number that contains all your numbers as factors.
Always greater than or equal to the largest number.
GCD (Greatest Common Divisor)
Looks DOWN at factors. It finds the largest number that fits inside all your numbers.
Always less than or equal to the smallest number.
Example: 12 and 18
Let's apply both to the numbers 12 and 18.
- GCD(12, 18) = 6. 6 is the biggest number that divides both 12 and 18.
- LCM(12, 18) = 36. 36 is the smallest number that both 12 and 18 divide into.
The Mathematical Relationship
There is a beautiful relationship connecting these two concepts:
LCM(a, b) × GCD(a, b) = a × b
Using our example: 36 × 6 = 216. And 12 × 18 = 216. It works perfectly!
When to Use Which?
Use LCM when:
- Adding or subtracting fractions (finding common denominator).
- Figuring out when repeating events will happen at the same time.
- Buying items sold in different package sizes (hot dogs vs buns).
Use GCD when:
- Simplifying fractions to their lowest terms.
- Splitting things into smaller, equal groups.
- Arranging items into rows or columns.