Special Right Triangles Explained
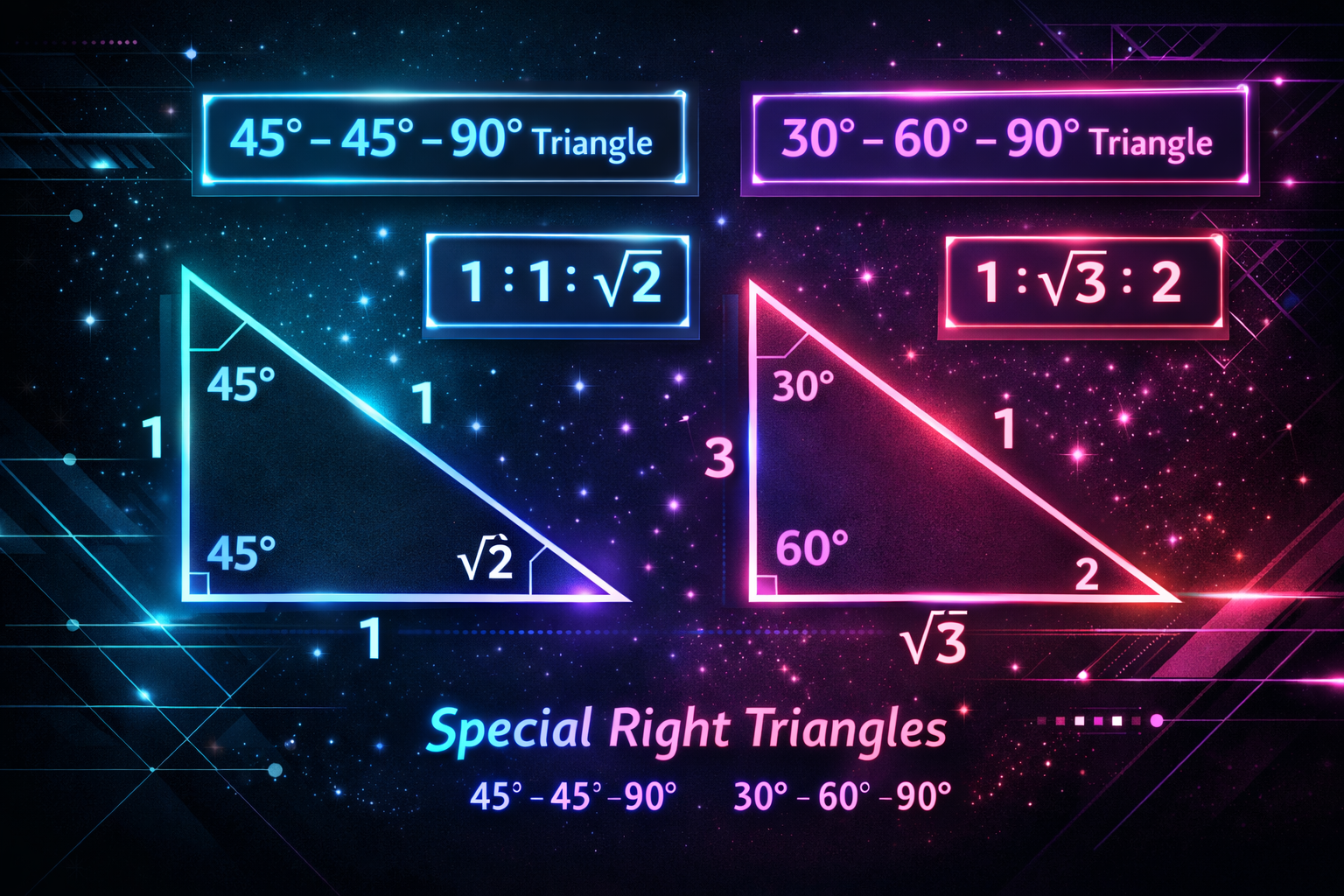
In geometry, special right triangles are right triangles with specific features that make calculations simple. Knowing the ratios of their sides allows you to find missing lengths without using the Pythagorean theorem or trigonometry.
The 45°-45°-90° Triangle
Also known as an isosceles right triangle, this triangle has two equal legs and two 45-degree angles.
The Ratio: 1 : 1 : √2
If the legs are length x, then:
- Leg 1 = x
- Leg 2 = x
- Hypotenuse = x√2
Example: If a leg is 5, the hypotenuse is simply 5√2 (approx 7.07).
The 30°-60°-90° Triangle
This triangle is half of an equilateral triangle. Its angles are 30°, 60°, and 90°.
The Ratio: 1 : √3 : 2
If the shortest side (opposite 30°) is x, then:
- Short Leg (opposite 30°) = x
- Long Leg (opposite 60°) = x√3
- Hypotenuse (opposite 90°) = 2x
Example: If the shortest side is 4:
- The long leg is 4√3 (approx 6.93).
- The hypotenuse is 2 × 4 = 8.
Why Are They Useful?
Special right triangles appear frequently in standardized tests (SAT, ACT) and real-world engineering. Memorizing these ratios saves valuable time and reduces calculation errors.
Summary Table
| Triangle Type | Leg 1 | Leg 2 | Hypotenuse |
|---|---|---|---|
| 45-45-90 | x | x | x√2 |
| 30-60-90 | x | x√3 | 2x |