Trigonometry Basics for Right Triangles

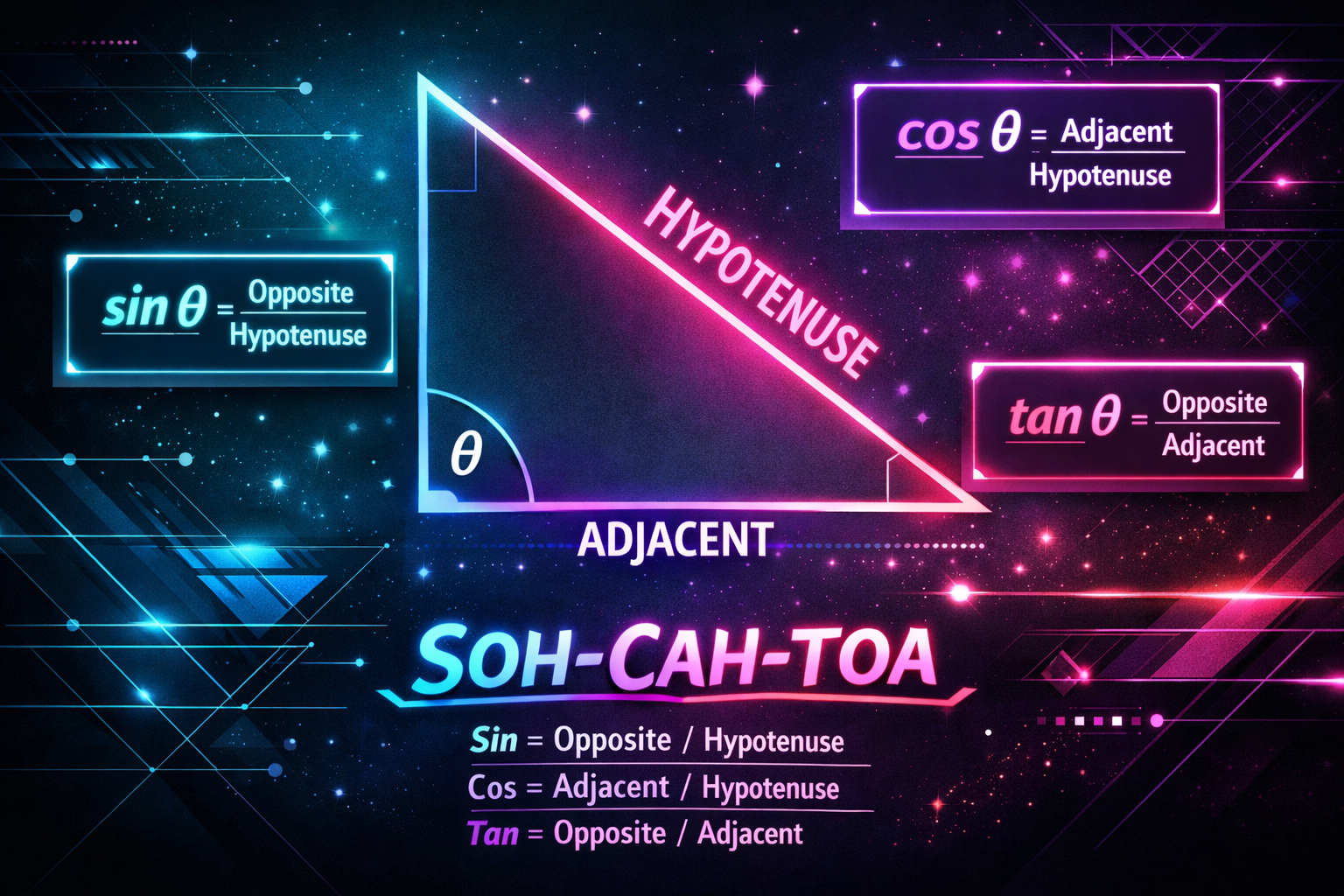
Trigonometry (from Greek "trigonon" for triangle and "metron" for measure) is the branch of mathematics that deals with the relationships between the sides and angles of triangles. For right triangles, three primary ratios form the foundation: Sine, Cosine, and Tangent.

Labeling the Triangle

Before defining the ratios, we must label the sides relative to a specific angle (let's call it θ or theta):

• Hypotenuse: The longest side, always opposite the 90° angle.
• Opposite: The side directly across from angle θ.
• Adjacent: The side next to angle θ (that isn't the hypotenuse).

The Three Ratios

Remembering with SOH CAH TOA

The mnemonic SOH CAH TOA is the easiest way to remember these definitions:

• SOH: Sine = Opposite / Hypotenuse
• CAH: Cosine = Adjacent / Hypotenuse
• TOA: Tangent = Opposite / Adjacent

Example Problem

Find the length of the side opposite a 30° angle if the hypotenuse is 10.

1. Identify the knowns: Angle = 30°, Hypotenuse = 10.
2. Identify the unknown: Opposite side.
3. Choose the ratio: We have Hypotenuse and want Opposite, so we use Sine (SOH).
4. Set up the equation: sin(30°) = Opposite / 10
5. Solve: 0.5 = Opposite / 10 → Opposite = 5.

Conclusion

Trigonometry allows us to solve for missing information in triangles that the Pythagorean theorem alone cannot handle. By mastering SOH CAH TOA, you can tackle a vast array of geometry problems.