Understanding the Pythagorean Theorem

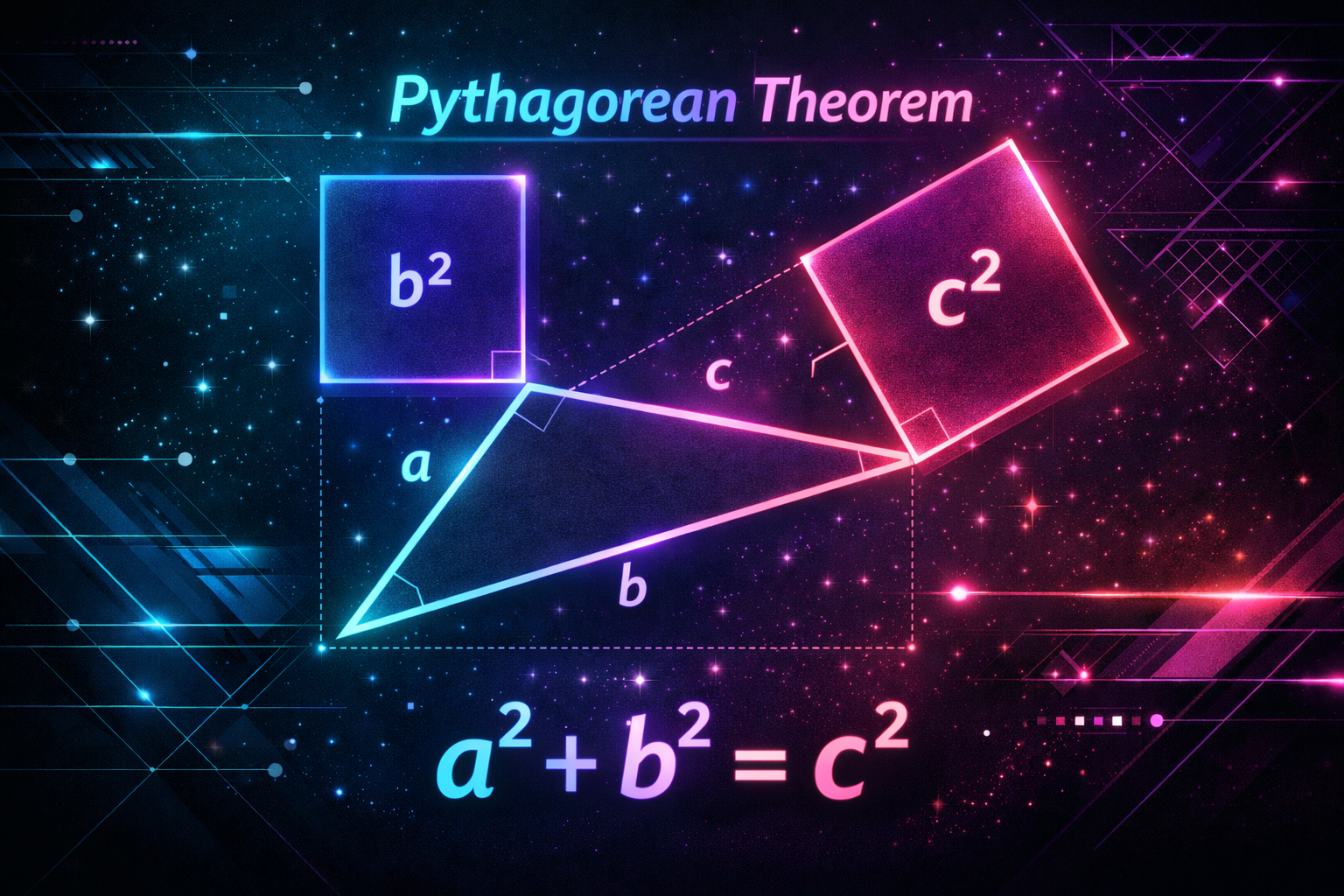
The Pythagorean theorem is one of the most famous and fundamental rules in geometry. It describes the relationship between the three sides of a right-angled triangle. Whether you're a student, an architect, or just a math enthusiast, understanding this theorem is essential.

What is the Pythagorean Theorem?

The theorem states that for any right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.

A Brief History

While the theorem is named after the ancient Greek mathematician Pythagoras (c. 570–495 BC), it was known to Babylonian and Indian mathematicians centuries earlier. However, Pythagoras is credited with the first recorded proof of the theorem.

How to Use the Theorem

You can use the Pythagorean theorem to find the length of any side of a right triangle if you know the lengths of the other two.

Example 1: Finding the Hypotenuse

Imagine a triangle with legs of length 3 and 4. To find the hypotenuse (c):

1. Plug the values into the formula: 3² + 4² = c²
2. Square the numbers: 9 + 16 = c²
3. Add them together: 25 = c²
4. Take the square root: c = √25 = 5

So, the hypotenuse is 5. This specific set of integers (3, 4, 5) is known as a Pythagorean triple.

Example 2: Finding a Leg

If you know the hypotenuse is 10 and one leg is 6, find the other leg (b):

1. Set up the equation: 6² + b² = 10²
2. Square the knowns: 36 + b² = 100
3. Subtract 36 from both sides: b² = 64
4. Take the square root: b = √64 = 8

Real-World Applications

• Construction: To ensure corners are perfectly square (90 degrees).
• Navigation: To calculate the shortest distance between two points.
• TV Screens: Screen sizes are measured diagonally, which is the hypotenuse of the rectangle.

Conclusion

The Pythagorean theorem is a powerful tool that connects algebra and geometry. Mastering it unlocks the ability to solve a wide range of problems in math and the real world.