What Is the Least Common Multiple (LCM)? Definition, Examples, and Uses

Definition of LCM

The Least Common Multiple (LCM) of two or more integers is the smallest positive integer that is divisible by each of the numbers. In other words, it is the first number that appears in the multiplication tables of all the numbers.

It is also known as the Lowest Common Multiple or, in the context of fractions, the Least Common Denominator (LCD).

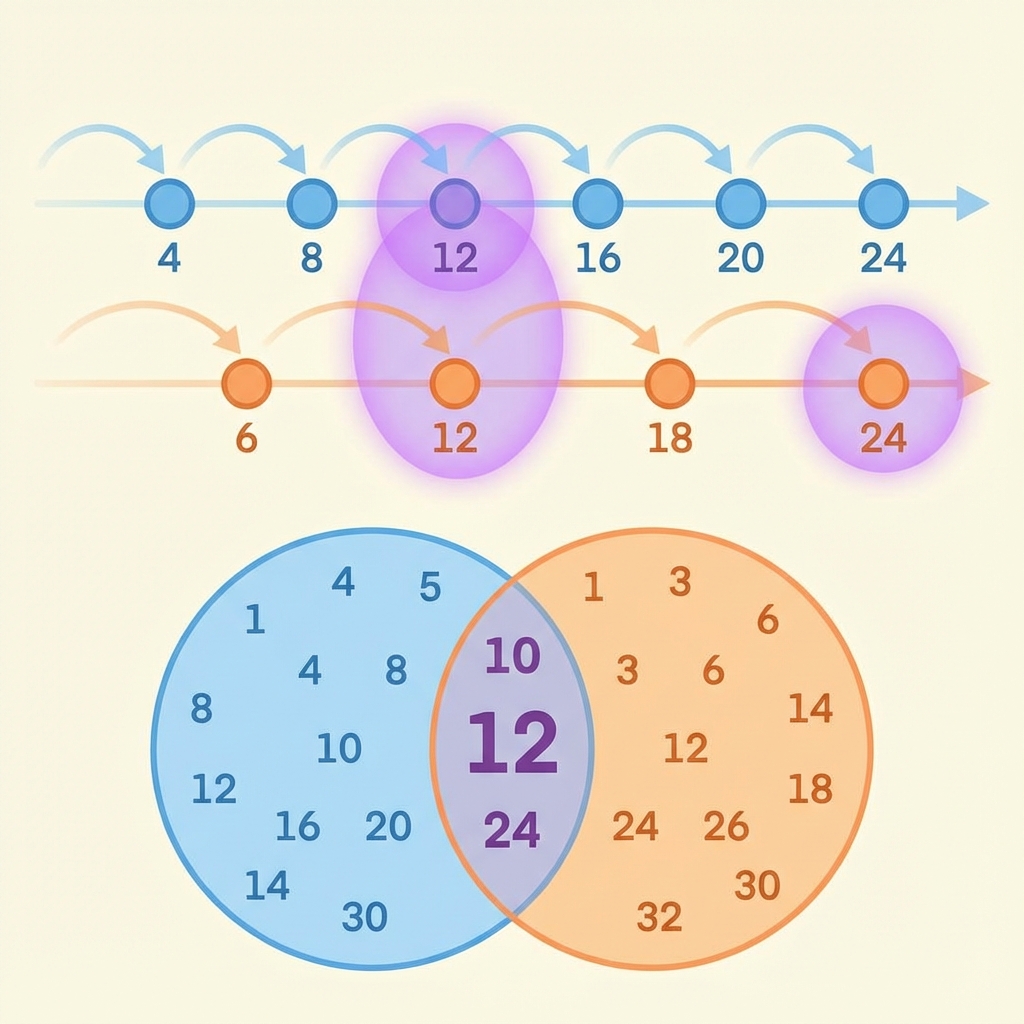
Visualizing the Concept

Imagine two frogs jumping along a number line. Frog A jumps 4 units at a time. Frog B jumps 6 units at a time.

• Frog A lands on: 4, 8, 12, 16, 20, 24...
• Frog B lands on: 6, 12, 18, 24, 30...

The first spot where they both land is 12. This is the LCM.

Real-World Examples

1. Hot Dogs and Buns

Hot dogs come in packs of 10. Buns come in packs of 8. What is the minimum number of packs you need to buy to have exactly one bun for every hot dog with none left over?

You need to find LCM(10, 8).
Multiples of 10: 10, 20, 30, 40...
Multiples of 8: 8, 16, 24, 32, 40...
LCM is 40. You need 4 packs of hot dogs (40 total) and 5 packs of buns (40 total).

2. Scheduling Work Shifts

One security guard checks a perimeter every 30 minutes. Another checks it every 45 minutes. If they both start at 8:00 AM, when will they meet again?

Find LCM(30, 45).
Multiples of 30: 30, 60, 90...
Multiples of 45: 45, 90...
LCM is 90 minutes. They will meet again in 1 hour and 30 minutes, at 9:30 AM.

Why It Matters

Understanding LCM helps in organizing cycles, optimizing resources (like the hot dog example), and solving complex fraction problems. It is a building block for higher-level algebra and number theory.