LCM Calculator

Calculate the Least Common Multiple (LCM) of two or more numbers instantly. Also known as Lowest Common Multiple or Least Common Denominator (LCD).

Perfect for adding fractions, solving math problems, and finding common denominators. Get step-by-step solutions with detailed explanations.

Share:

Enter at least two positive integers separated by commas

Why Use Our LCM Calculator?

Instant Results

Get the LCM of any numbers in milliseconds. Supports two or more numbers with step-by-step solutions showing the calculation process.

100% Accurate

Uses the proven LCM = (a × b) / GCD formula for guaranteed accuracy. Perfect for homework, exams, and professional work.

Learn & Understand

See step-by-step calculations to understand how the LCM is computed. Great for learning and verifying your manual calculations.

What is LCM (Least Common Multiple)?

The Least Common Multiple (LCM), also called the Lowest Common Multiple or Least Common Denominator (LCD) when working with fractions, is the smallest positive integer that is divisible by all given numbers without a remainder.

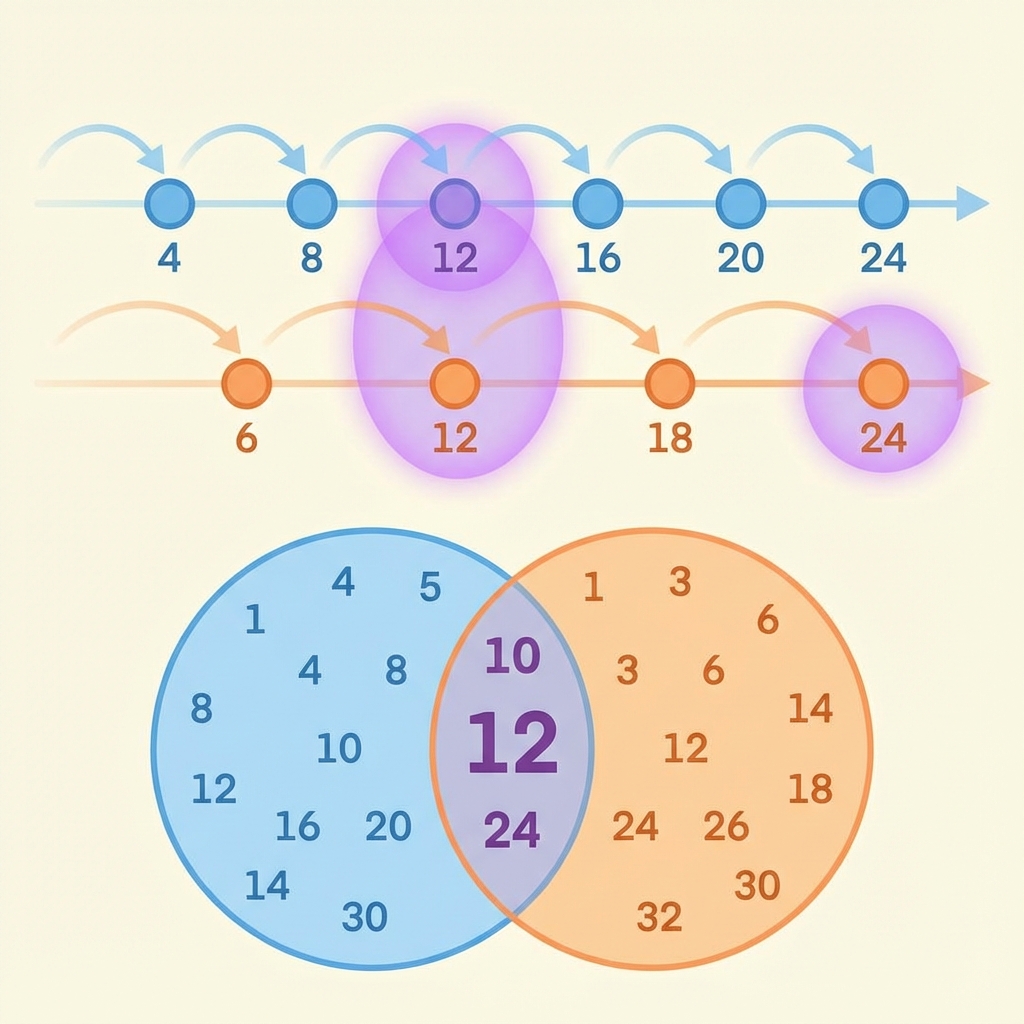
For example, consider the numbers 4 and 6:

  • Multiples of 4: 4, 8, 12, 16, 20, 24, 28...
  • Multiples of 6: 6, 12, 18, 24, 30...
  • Common multiples: 12, 24, 36...
  • Least Common Multiple: 12

The LCM is essential in mathematics for adding and subtracting fractions with different denominators, solving problems involving repeating events, and understanding number relationships.

How to Calculate LCM

Method 1: Listing Multiples (Small Numbers)

  1. List the multiples of each number
  2. Identify the common multiples
  3. Select the smallest common multiple

Example: LCM(4, 6)
Multiples of 4: 4, 8, 12, 16, 20, 24...
Multiples of 6: 6, 12, 18, 24, 30...
Common: 12, 24, 36...
LCM = 12

Method 2: Using GCD Formula (Most Efficient)

Use the relationship: LCM(a, b) = (a × b) / GCD(a, b)

  1. Find the GCD (Greatest Common Divisor) of the numbers
  2. Multiply the two numbers together
  3. Divide the product by the GCD

Example: LCM(12, 18)
GCD(12, 18) = 6
LCM = (12 × 18) / 6
LCM = 216 / 6
LCM = 36

Method 3: Prime Factorization

  1. Find the prime factorization of each number
  2. Take the highest power of each prime factor
  3. Multiply these together

Example: LCM(12, 18)
12 = 2² × 3
18 = 2 × 3²
LCM = 2² × 3² = 4 × 9
LCM = 36

For Multiple Numbers

To find LCM of more than two numbers:

  1. Find LCM of the first two numbers
  2. Find LCM of that result with the third number
  3. Continue for all remaining numbers

Example: LCM(4, 6, 8)
LCM(4, 6) = 12
LCM(12, 8) = 24
LCM = 24

Common Uses for LCM

➗ Adding Fractions

Find the LCM of denominators to get a common denominator for adding or subtracting fractions. Essential for fraction arithmetic and simplification.

📚 Math Homework

Essential for algebra, number theory, and arithmetic problems. Verify your manual calculations and understand the step-by-step process.

⏰ Scheduling & Cycles

Determine when repeating events will coincide. For example, if event A repeats every 4 days and event B every 6 days, they'll coincide every LCM(4,6) = 12 days.

📐 Measurement & Design

Find common measurements for tiling, patterns, and modular designs. Calculate the smallest size that accommodates different module sizes.

🎵 Music Theory

Determine when different rhythmic patterns align. Find common measures for polyrhythms and complex time signatures.

🔢 Number Theory

Fundamental concept in mathematics used in modular arithmetic, solving Diophantine equations, and understanding number relationships.

Related Calculators

View All
GCD Calculator
Fraction Calculator
Prime Factorization

Related Articles

LCM Calculator: How to Find the Least Common Multiple Step by Step

LCM Calculator: How to Find the Least Common Multiple Step by Step

Learn how to find the Least Common Multiple (LCM) with our step-by-step guide.

Learn More
What Is the Least Common Multiple (LCM)? Definition, Examples, and Uses

What Is the Least Common Multiple (LCM)? Definition, Examples, and Uses

Understand the concept of Least Common Multiple (LCM). Clear definitions and examples.

Learn More
LCM vs GCD: Key Differences with Practical Examples

LCM vs GCD: Key Differences with Practical Examples

Confused between LCM and GCD? Learn the key differences and when to use each one.

Learn More
View All Articles

Frequently Asked Questions

The Least Common Multiple (LCM), also called Lowest Common Multiple, is the smallest positive integer that is divisible by all given numbers. For example, the LCM of 4 and 6 is 12, because 12 is the smallest number that both 4 and 6 divide into evenly.
The most efficient method is using the formula: LCM(a, b) = (a × b) / GCD(a, b). First find the GCD (Greatest Common Divisor), then multiply the numbers and divide by the GCD. For multiple numbers, find the LCM of the first two, then find the LCM of that result with the third number, and so on.
LCM (Least Common Multiple) is the smallest number that all given numbers divide into, while GCD (Greatest Common Divisor) is the largest number that divides all given numbers. For example, for 12 and 18: LCM = 36, GCD = 6.
When adding fractions with different denominators, you need to find the LCM of the denominators to get a common denominator. For example, to add 1/4 + 1/6, find LCM(4, 6) = 12, then convert: 3/12 + 2/12 = 5/12.
Yes! To find the LCM of multiple numbers, first find the LCM of the first two numbers, then find the LCM of that result with the third number, and continue this process for all remaining numbers.
The LCM of two different prime numbers is always their product, because prime numbers have no common factors other than 1. For example, LCM(7, 11) = 77.
For any two numbers a and b, the relationship is: LCM(a, b) × GCD(a, b) = a × b. This formula is the basis for the most efficient method of calculating LCM.
No, the LCM is always greater than or equal to the largest number in the set. The only time LCM equals one of the numbers is when one number is a multiple of all the others.